
Kumpulan Gambar Jaring-Jaring Bangun Ruang Lengkap
Kubus
Kubus merupakan sebuah bangun ruang yang terbentuk oleh enam buah sisi yang saling berbatasan dan tiap sisi tersebut berbentuk persegi dengan ukuran yang sama besar. Sehingga apabila kita membuka sebuah kubus kemudian meletakkannya pada posisi mendatar akan diperoleh jaring-jaring kubus yang merupakan susunan dari enam buah persegi seperti terlihat pada gambar di bawah ini:
Balok
Sama halnya seperti kubus, balok juga terdiri dari enam buah sisi akan tetapi ukuran sisi pada balok berbeda. Ada 3 pasang sisi yang memiliki ukuran sama. Sehingga jika digambarkan, jaring-jaring dari sebuah balok akan menjadi seperti ini:
Prisma Segitiga
Berbeda dengan balok dan kubus, pada bangun ruang prisma segitiga ada dua buah sisi yang bentuknya berupa segitiga. Sehingga apabila digambarkan secara mendatar, jaring-jaring pada prisma segitiga akan terdiri dari dua buah segitiga dan tiga buah persegi atau persegi panjang.
Prisma Segi Lima
Untuk jaring-jaring prisma segilima, jumlah persegi atau persegi panjang yang muncul pada gambar akan lebih banyak. Jaring-jaringnya dibentuk oleh sebuah segilima dan lima buah persegi ataupun persegi panjang yang berderet.
Prisma Segi Enam
hampir sama dengan prisma segilima, hanya saja jaring-jaringnya akan terdiri dari satu buah bangun datar bersegi lima dan enam buah persegi atau persegi panjang yang berjajar. ini dia gambarnya:
Tabung
Untuk bangun ruang tabung gambar jaring-jaringnya cukup sederhana karena tabung hanya terdiri dari dua buah lingkaran yang sama besar sebagai tutup dan alasnya serta sebuah selimut yang jika dipotong akan membentuk sebuah persegi panjang. Gambar jaring-jaring tabung adalah sebagai berikut:
Kerucut
Kerucut memiliki jaring-jaring yang lebih sederhana lagi. Hanya terdiri ari sebuah segitiga yang memiliki alas berbentuk lengkungan, kemudian pada bagian bawah terdapat sebuah lingkaran yang menjadi alas kerucut. Berikut gambar jaring-jaring kerucut:
Limas Segitiga
Karena limas segitiga dibentuk oleh empat buah sisi yang semuanya berbentuk segitiga, maka jaring-jaringnya akan terdiri dari empat buah segitiga seperti pada gambar berikut ini:
Limas Segi Empat
Berbeda dengan limas segitiga, untuk limas segiempat, gambar jaring-jaringnya berupa sebuah persegi atau persegi panjang yang pada tiap sisinya berbatasan dengan sisi berbentuk segitiga seperti terlihat pada gambar ini:
Limas Segi Lima
limas segi lima terbentuk oleh sebuah alas berbentuk segilima dimana pada tiap-tiap sisinya berbatasan dengan 5 buah segitiga. maka jaring-jaring dari bangun ruang limas segilima akan tampak seperti sebuah bintang.
Bola
Untuk bagun ruang bola kita tidak bisa membuat jaring-jaringnya karena bentuk lengkung 3 dimensi pada bola tidak dapat diubah ke dalam bentuk datar atau bentuk 2 dimensi secara sempurna, maka tidak ada gambar jaring-jaring untuk bangun ruang bola. Tapi di bawah ini ada sedikit ilustrasi jaring-jaring bola.
Gambar : Pola jaring-jaring bola Sumber : rustamaji.net
Demikian penjelasan singkat mengenai jaring-jaring dari setiap bangun ruang serta Gambar Jaring-Jaring Bangun Ruang Lengkap yang dapat kalian cermati dan hafalkan karena biasanya pada ujian nasional akan muncul soal-soal yang melampirkan gambar jaring-jaring dari sebuah bangun ruang. Untuk mempelajari lebih jauh mengenai bangun ruang kalian bisa membaca Materi Ciri dan Sifat-sifat Bangun Ruang.
Materi Ciri dan Sifat-Sifat Bangun Ruang Lengkap
Sifat-Sifat Bangun Ruang - Bangun ruang atau biasa disebut juga sebagai bangunan tiga dimensi merupakan jenis bangun yang memiliki ruang serta sisi-sisi yang membatasinya. Jumlah serta bentuk dari setiap sisi yang ada menjadi ciri khas tersendiri dari sebuah bangun ruang. Karena bentuk dan jumlah rusuknya berbeda, maka setiap bangun ruang memiliki karakteristik sendiri yang menjadi ciri-ciri atau pun sifat dari bangun ruang tersebut.
Seperti halnya bangun datar yang memiliki sifat-sifat bangun datar dan rumusnya tersendiri, bangun ruang juga tentu memilikinya. Untuk mengetahui sifat dari masing-masing bangun ruang, kalian bisa menyimak dalam penjelasan yang telah dirangkum oleh tim
rumus matematika dasar berikut ini:
Penjelasan Sifat-Sifat Berbagai Jenis Bangun Ruang
Sifat Bangun Ruang Kubus
Sifat-sifat yang menjadi ciri khas dari kubus adalah:
- mempunyai enam buah sisi dengan ukuran dan bentuk yang sama persis.
- jumlah rusuk yang membentuknya ada 12 buah dengan ukuran yang sama persis.
- rusuk tersebut saling bertemu dan membentuk delapan buah sudut yang besarnya sama (900)
Sifat Bangun Ruang Balok
Sifat-sifat yang menjadi ciri khas dari balok adalah:
- mempunyai empat buah sisi dengan bentuk persegi panjang
- ada dua buah sisi yang memiliki bentuk sama.
- terdapat empat buah rusuk yang memiliki ukuran sama persis.
Sifat Bangun Ruang Tabung
Sifat-sifat yang menjadi ciri khas tabung adalah:
- memiliki sisi alas dan atas yang bentuknya sama berupa lingkaran.
- mempunyai sisi lengkung atau selimut yang menghubungkan sisi alas dan atas.
Sifat Bangun Ruang Kerucut
Sifat-sifat yang menjadi ciri khas kerucut adalah:
- mempunyai sebuah alas yang bentuknya lingkaran
- mempunyai titik puncak atas
- memiliki selimut (sisi) yang berbentuk lengkung.
Sifat Bangun Ruang Limas Segitiga
Sifat-sifat yang menjadi ciri khas dari limas segitiga adalah:
- memiliki alas yang berbentuk segitiga
- terdapat tiga buah sisi yang bentuknya segitiga
- terbentuk dari enam buah rusuk
- mempunyai tiga rusuk yang sama persis ukurannya.
- mempunyai titik puncak atas.
Sifat Bangun Ruang Limas Segiempat
Sifat-sifat yang menjadi ciri khas dari limas segiempat adalah:
- bentuk alasnya berupa segiempat
- mempunyai empat buah sisi yang bentuknya segitiga
- ada empat buah rusuk yang ukurannya sama persis.
- mempunyai titik puncak atas
Sifat Bangun Ruang Prisma
Sifat-sifat yang menjadi ciri khas dari prisma adalah:
- mempunyai tiga buah sisi, dua buah sisi berbentuk segitiga dan tiga buah sisi berbentuk persegi panjang.
- mempunyai 6 buah titik sudut
- jumlah rusuknya ada sembilan
Sifat Bangun Ruang Bola
Sifat-sifat yang menjadi ciri khas dari bola adalah:
- hanya memiliki satu buah sisi
- tidak mempunyai titik sudut
- hanya mempunyai sebuah sisi lengkung yang tertutup
Kubus adalah bangun ruang yang dibatasi oleh enam bidang sisi yang berbentuk bujur sangkar.
a. Luas Permukaan kubus
L= 6 a2
b. Volume Kubus
V = a x a x a atau V = a3
2. Balok
Balok adalah bangun ruang yang dibatasi oleh enam bidang yang berbentuk persegi panjang dan sepasang-sepasang kongruen.
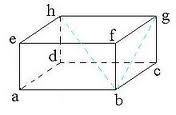
Keterangan :
p = panjang balok
l =lebar balok
t = tinggi balok
a. Luas balok:
L = 2 (p.l +p.t + l.t)
b. Volume balok:
V = p x l x t
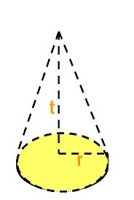
3.Tabung (silinder)
Tabung adalah bangun ruang yang dibatasi oleh dua sisi yang kongruen dan sejajar yang berbentuk lingkaran serta sebuah sisi lengkung.
Keterangan:
r = jari-jari tutup/alas tabung t = tinggi tabung
Volume tabung = luas alas x tinggi
Luas alas = luas lingkaran = πr2
Volume tabung = π r 2 t
Keliling lingkaran alas/tutup = 2πr
Luas Selimut= 2πrt
Luas Permukaan Tabung = 2 x luas alas + Luas selimut tabung
Luas Permukaan Tabung = 2 (π r 2 )+ 2 π r t = 2 π r ( r + t )
4. Kerucut
Kerucut adalah bangun ruang yang dibatasi oleh sebuah sisi alas berbentuk lingkaran dan sebuah sisi lengkung.
Keterangan:
r = jari-jari alas kerucut t = tinggi kerucut
Luas selimut = π x r x s
Luas alas = π x r 2
Luas Permukaan kerucut = Luas alas + Luas Selimut
Luas Permukaan kerucut = πr2 + πrs = π r (r + s)
Volume Kerucut =1/3 x Luas alas x tinggi = 1/3 π r2 t
5. Prisma
Prisma adalah bangun ruang yang dibatasi oleh dua buah bidang sejajar dimana bidang-bidang sejajar tersebut merupakan bidang atas dan bidang atas (tutup).
Rumus-rumus pada prisma:
Luas Permukaan Prisma
Luas = (2 x luas alas) + luas sisi tegak
V = L alas x t
Volume Prisma
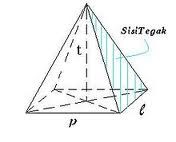
6.Limas
Limas adalah bangun ruang yang dibatasi oleh sebuah segi sebagai bidang alas dan beberapa bidang tegak berbentuk segitiga.
Luas permukaan Limas
L = luas alas + luas sisi tegak
Volume Limas :
Volume = luas alas x tinggi x 1/3
7. Bola
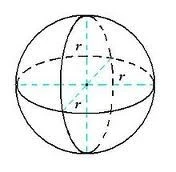
r = jari-jari bola
Luas Permukaan bola
Luas = L = 4 × π × r²
Volume Bola = V = 4/3 × π × r³
Contoh 1: Cara Menghitung Volume Bola dan Luas Permukaan Bola
1.1 Hitunglah volume bola yang mempunyai jari-jari 9 cm berikut ...
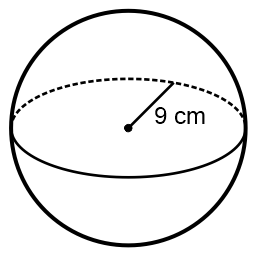
Diketahui:
r = 9 cm
Karena r bukan kelipatan 7, maka digunakan nilai π = 3,14
Ditanya:
Volume Bola (V)
Penyelesaian:
V = 4/3 × π × r³
V = 4/3 × 3,14 × (9 cm)³
V = 4/3 × 3,14 × (9 cm × 9 cm × 9 cm)
V = 4/3 × 3,14 × 729 cm³
V = 3052,08 cm³
Jadi, volume bola tersebut adalah 3052,08 cm³
1.2 Hitunglah luas permukaan bola yang mempunyai jari-jari 14 cm berikut ...
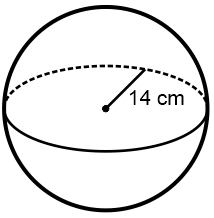
Diketahui:
r = 14 cm
Karena r kelipatan 7, maka digunakan nilai π = 22/7
Ditanya:
Luas permukaan bola (L)
Penyelesaian:
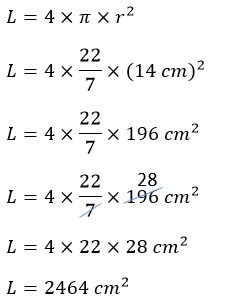
Jadi, luas permukaan bola 2464 cm²
Contoh 2: Cara Menghitung Jari-Jari Bola Jika Diketahui Volume
Hitunglah panjang jari-jari bola yang mempunyai volume 38.808 cm³ ...
Diketahui:
V = 38.808 cm³
Karena volume bola habis dibagi 7 yaitu 38.808 ÷ 7 = 5544 (hasil tidak memuat angka desimal), maka digunakan nilai π = 22/7.
Ditanya:
Jari-jari bola (r)
Penyelesaian:
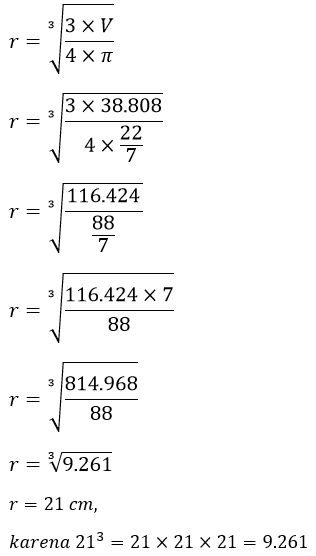
Jadi, jari-jari bola adalah 21 cm.
Contoh 3: Cara Menghitung Jari-Jari Bola Jika Diketahui Luas
Hitunglah jari-jari bola yang mempunyai luas permukaan 616 cm² ...
Diketahui:
L = 616 cm²
Karena luas bola habis dibagi 7 yaitu 616 ÷ 7 = 88 (hasil tidak memuat angka desimal), maka digunakan nilai π = 22/7.
Ditanya:
Jari-jari bola (r)
Penyelesaian:
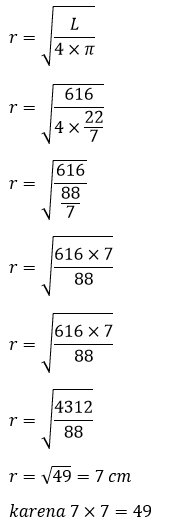
Jadi, jari-jari bola adalah 7 cm.
Contoh soal :
1. Suatu tabung yang diameternya 14 cm dan tingginya 8 cm. berapakah volumenya?
Pembahasan :
diketahui : d= 14 cm dan t= 8 cmr = ½
d =1/2 . 14 = 7 cm
V = πr2t = 22/7 x (7x 7) x 8 = 22 . 7 . 8 = 1.232 cm3
2. Diketahui volume tabung 169,56 cm3 dengan tinggi 6 cm. berapakah jari-jarinya?
Pembahasan :
diketahui : V= 169,56 cm3 dan t= 6 cm
V = πr2t 169,56 cm3 = 3,14 x r2 x 6169,56 cm3
= 18,84 r2r2
= 169,56/18,84r2 = 9r = 3 cm
3. Diketahui volume tabung 1540 cm3 dengan jari-jari 7 cm. berapakah tingginya?
Pembahasan :
diketahui : V= 1540 cm3 dan r = 7 cm
V = πr2t1540 cm3
= 22/7 x (7 x 7) x t1540 cm3
= 154 tt = 1540 cm3 / 154t = 10 cm
4. sebuah tabung mempunyai jari-jarinya 14cm dan tinggi tabung adalah 10 cm , maka tentukanlah volume setengah tabung :
pembahasan :
diketahui : r = 14 cm dan t= 10 cm
volume setengah tabung = 1/2 πr2t= 1/2 x 22/7 x 14 x 14 x10
= 3080 cm3
Sumber :
http://vivianadesisetiani89.blogspot.com
https://www.advernesia.com





















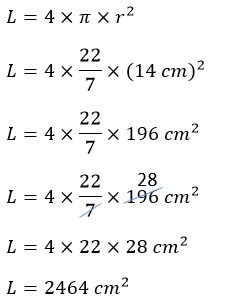
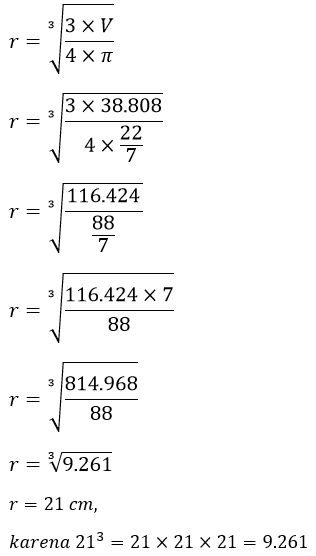
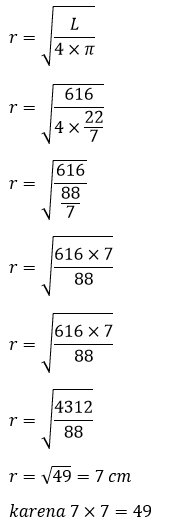


0 Komentar